Biography

I am an assistant professor in the Theory group of the Laboratory of Solid State Physics of the University Paris-Saclay. My main research interests are ab-initio theories of condensed matter, topological states of matter, and strongly correlated electron systems.

Applications for internships in 1st or 2nd year of Master are always welcome. Please feel free to contact me if you have any question. You can find some of my internship proposals on the website of the ICFP. There is currently no postdoc opening in my group.

Topological states in interacting systems

We study topological states of matter in contexts where it is necessary to go beyond standard band theory, in particular when correlations are important. In a recent preprint, we defined the zeros surface, a set of points in reciprocal space formed by the zeros of diagonal elements of the Green’s function, and showed that it allows one to directly visualise the Z₂ topological invariants in inversion-symmetric systems.

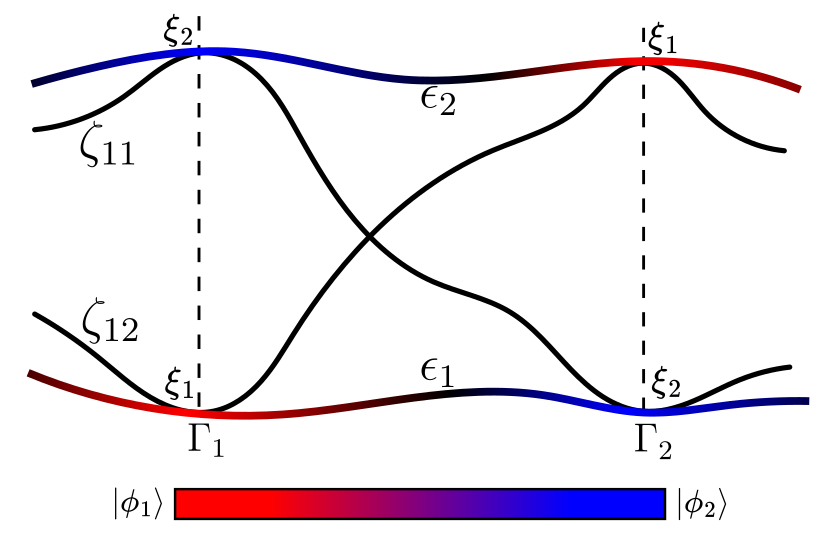
Publication

• F. Simon and C. Morice, arXiv:2504.00800.

Ab-initio theories of condensed matter

We collaborate with experimental teams on various systems, such as two-dimensional Van der Waals heterostructures and compounds exhibiting charge density wave phases. Using density functional theory (DFT) and many-body perturbation theory, in the framework of the GW approximation, we calculate observables which enhance our understanding of the measured physics.

Publications

• S. D. C. Roscam Abbing, F. Campi, B. de Keijzer, C. Morice, Z.-Y. Zhang, M. L. S. van der Geest, P. M. Kraus, Nat. Comm. 15, 8335 (2024).
• Y. Sun, C. Morice, D. Garrot, R. Weil, K. Watanabe, T. Taniguchi, M. Monteverde and A. D. Chepelianskii, Adv. Electron. Mater. 10, 2400211 (2024).
• J. Groefsema, X. Feng, C. Morice, Y. Huang, E. van Heumen, Phys. Rev. Materials 6, 115402 (2022).
• B. van der Linden, T. Hogenelst, R. Bliem, K. Dohnalová and C. Morice, J. Phys.: Condens. Matter 34, 425403 (2022).
• X.Feng, J. Henke, C. Morice, C. J. Sayers, E. Da Como, J. van Wezel and E. van Heumen, Phys. Rev. B 104, 165134 (2021).

Gravitational analogues

We designed low-dimensional electronic models, related to Weyl semimetals, which mimic some of the properties of gravitational systems. In particular, we studied the dynamics of wave packets of electrons in 1D and 2D lattice models, the spectral properties of these models, and ground-state thermalisation near a gravitational horizon.

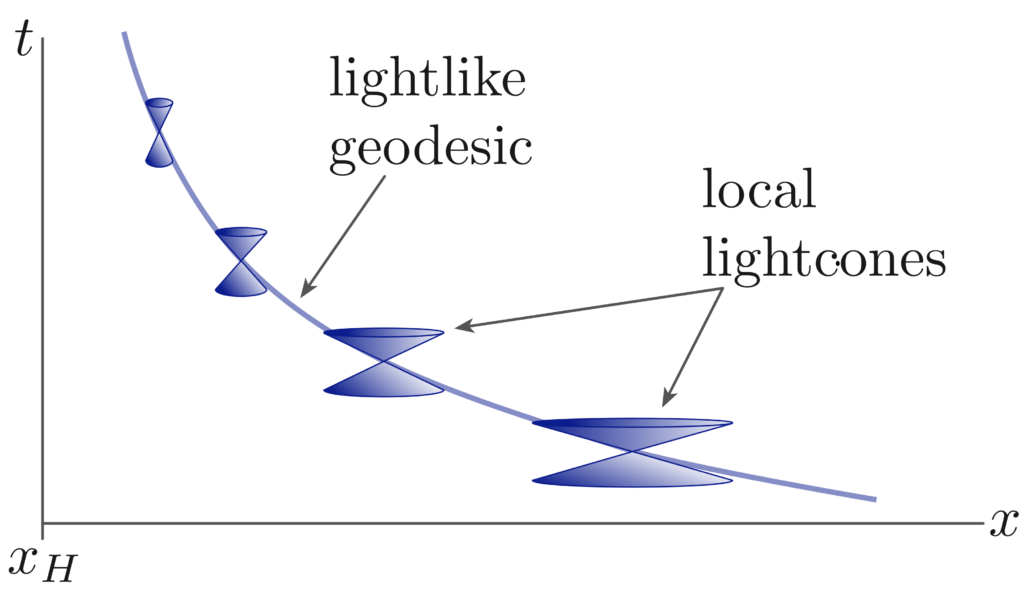
Publications

• V. Könye, L. Mertens, C. Morice, D. Chernyavsky, A. G. Moghaddam, J. van Wezel and J. van den Brink, Phys. Rev. B 107, L201406 (2023).
• L. Mertens, A. G. Moghaddam, D. Chernyavsky, C. Morice, J. van den Brink and J. van Wezel, Phys. Rev. Research 4, 043084 (2022).
• V. Könye, C. Morice, D. Chernyavsky, A. G. Moghaddam, J. van den Brink and J. van Wezel, Phys. Rev. Research 4, 033237 (2022).
• C. Morice, D. Chernyavsky, J. van Wezel, J. van den Brink and A. Moghaddam, SciPost Phys. Core 5, 042 (2022).
• A. G. Moghaddam, D. Chernyavsky, C. Morice, J. van Wezel, and J. van den Brink, SciPost Phys. 11, 109 (2021).
• C. Morice, A. G. Moghaddam, D. Chernyavsky, J. van Wezel, and J. van den Brink, Phys. Rev. Res. Lett. 3, L022022 (2021).

Finite-size topological insulators

We investigate the influence of finite thickness on properties of topological insulators.

We studied a minimal model for topological insulators in a slab geometry. One parameter of our model, namely the Dirac velocity perpendicular to the slab, distinguishes between two qualitatively distinct situations: when it is zero, we find that the topological invariants of the 3D system can be entirely deduced from properties of the slab. However when it is not zero, a new phase arises, with surface states but without band inversion. We also investigated this model for large dispersions perpendicularly to the slab and unveiled a regime where the slab displays non-trivial topological invariants but nonetheless extrapolates towards a trivial 3D state.

The new phase which displays surface states without band inversion is localised close to topological phase transitions. We therefore studied ZrTe₅, which was shown to be a strong topological insulator, on the border of a weak topological insulating phase. We derived a model for this material fitted to ab-initio calculations and showed that it matches many experimental signatures, including optical, transport, and spectroscopic results.

Publications

• C. Morice, E. Lettl, T. Kopp, and A. P. Kampf, Phys. Rev. B 102, 155138 (2020).
• C. Morice, T. Kopp, and A. P. Kampf, Phys. Rev. B 100, 235427 (2019).

I teach physics in various tracks of the University Paris-Saclay.

Lectures

Topology and Mesoscopic Physics — Quantum Light Matter and Nano Sciences (MSc, 2nd year)
Numerical Physics — License Double Diplôme Maths-Physique (BSc, 2nd year)

Exercises classes

Quantum mechanics — CentraleSupélec (BSc, 3rd year)
Statistical Physics — Magistère de Physique Fondamentale (BSc, 3rd year)
Classical Mechanics — Magistère de Physique Fondamentale (BSc, 3rd year)

Practicals

Numerical Physics — ENS Paris-Saclay (BSc, 3rd year)
Density Functional Theory — Master in Materials Sciences (MSc, 1st year)

Contact

corentin.morice@universite-paris-saclay.fr

+33 (0) 1 69 15 45 73

1 rue Nicolas Appert, Bâtiment 510, 91405 Orsay Cedex, France

Exercises classes

Exercise classes for the Statistical Physics course of the 3rd year of the Fundamental Physics bachelor in the University Paris-Saclay.

Contact

• corentin.morice@universite-paris-saclay.fr
• +33 (0) 1 69 15 45 73
• 1 rue Nicolas Appert, Bâtiment 510, 91405 Orsay Cedex, France
• How to reach the LPS

Contact

• corentin.morice@universite-paris-saclay.fr
• +33 (0) 1 69 15 45 73
• 1 rue Nicolas Appert, Bâtiment 510, 91405 Orsay Cedex, France
• How to reach the LPS

Contact

• corentin.morice@universite-paris-saclay.fr
• +33 (0) 1 69 15 45 73
• 1 rue Nicolas Appert, Bâtiment 510, 91405 Orsay Cedex, France
• How to reach the LPS

Contact

• corentin.morice@universite-paris-saclay.fr
• +33 (0) 1 69 15 45 73
• 1 rue Nicolas Appert, Bâtiment 510, 91405 Orsay Cedex, France
• How to reach the LPS